Die Cent-Skala wurde 1875 von Alexander J. Ellis entwickelt. Er verwendete sie, um Ton- und Stimmungssysteme unterschiedlicher Kulturen zu vergleichen. In diesem Artikel lernen Sie, wie die Skala definiert wird und wie man mit ihr rechnet.
Definition
Die Cent-Skala unterteilt die Oktave in 12 gleichstufige Halbtonschritte. Jeder Halbtonschritt entspricht dabei 100 Cent. So hat jede Oktave 1200 Cent, unabhängig davon, in welchem Frequenzbereich sie sich befindet.
Die DIN-Norm 13320 definiert das Maß von 1 Cent als Frequenzintervall, welches ein Verhältnis von \(2^ \frac {1} {1200}\) beträgt. Das Verhältnis zwischen zwei Frequenzen lässt sich so mit \(c = 1200 \times \mathrm{log}_2(f_1/f_2)\) definieren.
Hauptsächlich wird mit Cent die Größe verschiedener Intervalle verglichen. Dabei wird den beiden Tönen des Intervalls kein spezifischer Wert in Cent zugeordnet, da nur der Abstand der zwei Töne in Cent angegeben wird. Dennoch ist es möglich, auch spezifischen Tönen, bzw. Frequenzen einen Cent-Wert zuzuordnen. Dafür gilt folgende Norm: 1 Hz = 0 Cent.
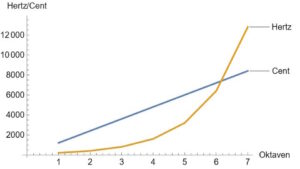
In diesem Bild können Sie gut erkennen, dass sich die Cent-Skala linear verhält. Dem gegenüber steht das Frequenzmaß Hertz, welches von Oktave zu Oktave exponentiell größere Werte annimmt. Grafik: Marie-Luise Hartmann
Im Gegensatz zu dem Frequenzmaß Hertz berücksichtigt die Cent-Skala bereits in ihrer Definition, dass die Tonhöhenwahrnehmung des Menschen eher logarithmisch verläuft. Das Frequenzmaß Hz definiert hingegen die Anzahl der periodischen Schwingungen pro Sekunde wieder. Betrachtet man die Hz von aufsteigenden Oktaven, zeigt sich, dass die Frequenzabstände auf der Skala immer größer werden (400 Hz – 800 Hz – 1600 Hz – 3200 Hz – etc.). Bei der Cent-Skala entspricht jede Oktave entspricht jede Oktave jedoch 1200 Cent (1200 Cent – 2400 Cent – 3600 Cent – 4800 Cent – etc.).
Durch diesen linearen Verlauf der Cent-Skala lassen sich Intervalle über den ganzen Tonraum hinweg leichter vergleichen, da ein gleich großer Unterschied zwischen zwei Zahlen der Cent-Skala auch einen gleich großen Tonunterschied im wahrgenommenen Intervall bedeutet.
Rechnen mit der Cent-Skala
Mit der Skala kann man auf zwei verschiedene Arten rechnen, die jeweils unterschiedliche Zielsetzungen haben. Zum einen können Sie das Frequenzverhältnis (in Hz) zwischen zwei Tönen in Cents umrechnen. Andererseits können Sie berechnen, in welcher Frequenz (in Hz) ein um beispielsweise 120 Cent höherer Ton schwingt. Beide Rechenwege sind auch mit der Verwendung des absoluten Cents möglich.
Frequenzverhältnisse in Cent umrechnen
Im Folgenden wollen wir das Frequenzverhältnis einer reinen Quinte in Cents umwandeln. Die reine Quinte hat ein Frequenzverhältnis von 3:2. Für die reine Quinte benutzen wir das Intervall zwischen den Tönen c‘ (261,63 Hz) und g‘ (392,445 Hz). Die beiden Frequenzen können als Bruch in ihr Verhältnis gesetzt werden:
\(\frac {g‘}{c‘} = \frac {392,445 Hz}{261,63 Hz}\)Dieses Verhältnis lässt sich nun in die während der Definition genannten Formel einsetzen:
\(c = 1200 \times \mathrm{log}_2(f_2/f_1)\newline\) \(c = 1200 \times \mathrm{log}_2(392,455/261,63)\newline\) \(c = 701,955\)So besteht das Frequenzverhältnis einer reinen Quinte aus 701,955 Cents. Statt 261,63 Hz und 392,445 Hz können Sie natürlich auch 2 und 3 einsetzen, denn die Einheit „Hz“ kürzt sich raus und 392,455/261,63 ≈ 3/2 = reine Quint.
Werte der Cent-Skala in Hertz umrechnen
Im Folgenden wollen wir errechnen, in welcher Frequenz (Hz) ein Ton schwingt, der 350 Cent höher als das c‘ (261,63 Hz) ist. Bei unserem bekannten Ton c‘ handelt es sich somit um unsere erste Frequenz \(f_1/latex]. Die zweite unbekannte Frequenz [latex]f_2\) gilt es hier herauszufinden.
Um die zweite Frequenz zu berechnen, verwende sie die folgende Formel:
\(f_2 = f_1\times 2^ \frac{c}{1200}\)
So sieht die Formel mit den eingesetzten Zahlen aus:
\(f_2 = 261,63\times 2^ \frac{350}{1200}\)\( f_2 = 320,249\)
Somit klingt ein Ton, welcher 350 Cents höher als das c‘ (261,63 Hz) ist, mit einer Frequenz von 320,249 Hz.
Cents, Frequenz und Stimmungssysteme
Besonders in den letzten Jahrhunderten ist die gleichstufige Stimmung von Musikinstrumenten weit verbreitet. Gehen Sie auf dem Keyboard eine Taste weiter, erklingt in der Regel ein Ton, deren Grundfrequenz 100 Cent höher ist. Dadurch ist zum Beispiel die Quinte nur 700 Cents groß, im Gegensatz zur reinen Quinte von 701,955 Cents. Das muss aber nicht so sein. Bei anderen Stimmungen, wie der pytagoreische Stimmung, oder Werckmeister-Stimmung, sind nicht alle Nachbarn genau 100 Cents voneinander entfernt. So können Sie zum Beispiel reine Quinten erzeugen. Um die Unterschiede zwischen Stimmungssystemen zu erfassen, reichen Frequenz und klassische Intervalle kaum aus. Die Cent-Skala schafft Abhilfe. Sie ist zudem besonders wichtig in der Erforschung und im Vergleich verschiedener Musikkulturen. In welchem historischen Kontext die Entwicklung der Cent-Skala stattfand, können Sie in meinem Artikel zur Vergleichenden Musikwissenschaft lesen.
