Die Shepard-Tonleiter besitzt die spannende Eigenschaft, scheinbar unendlich an- oder abzusteigen. Viele kennen sie auch als „Shepard-Skala“ oder „unendliche Tonleiter“. Wie Sie eine Shepard-Tonleiter aufbauen können, sowie Hörbeispiele für die Tonleiter, zeigt dieser Artikel.
Die Entdeckung der Shepard-Tonleiter
Die Shepard-Tonleiter wurde nach Roger N. Shepard benannt. Er veröffentlichte 1969 den Fachartikel Circularity in Judgments of Relative Pitch, in welchem er diese Illusion erstmals beschrieb.
Diese Täuschung der Shepard-Tonleiter gehört zu den auditiven Illusionen, welche das Gegenstück der besser bekannten visuellen Illusionen bilden. Die Penrose-Treppe ist ein Beispiel für unendliche fortlaufende visuelle Illusion. Auditive Illusionen werden häufig auch als akustische Täuschungen oder auditorische Illusionen bezeichnet, wobei die Begriffe auditive oder auditorische Illusionen in der Wissenschaft genutzt werden.
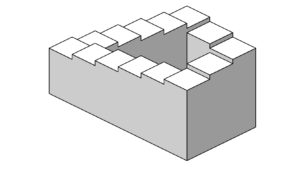
Visuelle Illusion: Die Penrose-Treppe führt, wie die Shepard-Tonleiter, unendlich auf- oder abwärts
Bild: Sakurambo, Gemeinfrei
Shepard untersuchte in verschiedenen Versuchen, wie komplexe Töne wahrgenommen werden. Komplexe Töne bestehen aus überlagerten Sinustönen. Dabei handelt es sich um einen Grundton und dessen ganzzahlige Vielfache (Obertöne). Shepard verwendete komplexe Töne, dessen Obertöne nur die vielfachen Oktaven des Grundtons waren. Dabei stellte er fest, dass Proband’innen die Tonhöhe solcher Töne unterscheiden können, aber es ihnen trotzdem schwerfällt, die Oktavlage des Tons zu benennen. Auch wenn die komplexen Töne zu einer Tonleiter aneinandergereiht wurden, nahmen Hörer’innen eine immer weiter aufsteigende Tonleiter wahr. Einige waren von diesem scheinbar unendlichen Anstieg verwirrt, anderen fiel dies wiederum nicht auf.
Aufbau der Shepard-Tonleiter
Die einzelnen Töne der Tonleiter werden als Shepard-Töne bezeichnet. Das Besondere an einem Shepard-Ton ist, dass dieser nur aus Sinustönen im Oktavabstand besteht. Ein Shepard-Ton mit der Grundfrequenz 55 Hz hat die Obertöne mit den Frequenzen 110 Hz, 220 Hz, 440 Hz, 880 Hz, also 55 Hz · 2n. Diese Frequenzen entsprechen alle der Note A. Die einzelnen Sinustöne haben jeweils unterschiedliche Lautstärken (Amplituden L). Sie werden durch eine Hüllkurve (siehe Abbildung) definiert. Die genau Form der Hüllkurve spielt dabei keine große Rolle. Wichtig ist nur, dass der Hochpunkt bei den mittleren Frequenzen liegt und die Kurve zu den Rändern hin abfällt. Das heißt, dass die tiefen und hohen Komponenten eines Shepard-Tons leiser als die mittleren Frequenzen sind.
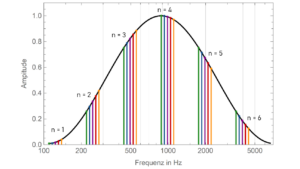
Die ersten fünf Töne einer Shepard-Tonleiter. Schwarz: Hüllkurve; mmax = 12; nmax = 6; Grafik: Hannah Mayer
Mit den folgenden Formeln werden die Frequenzen f(m,n) der einzelnen Komponenten n und deren Amplitude L bestimmt. Dabei ist n jeweils eine Komponente eines Tons m der Tonleiter:
\(f(m,n)=f_{\mathrm{min}} \cdot 2^{\frac{(n-1)\cdot m_{\mathrm{max}}+m-1}{m_{\mathrm{max}}}}\)
\(L(m,n)=L_{\mathrm{min}}+(L_{\mathrm{max}}-L_{\mathrm{min}})\cdot (1-\cos \theta)\)
mit \(\theta(m,n)=2\pi \cdot \frac{(n-1)\cdot m_{\mathrm{max}}+m-1}{m_{\mathrm{max}} \cdot n_{\mathrm{max}}} \)
- m: m-te Ton der Tonleiter
- n: n-te Komponente des m-ten Tons
- fmin: Niedrigste Frequenz des tiefsten Tons der gesamten Tonleiter
- mmax: Anzahl der Shepard-Töne pro Tonleiter (für Tonleiter in Halbtonschritten mmax = 12)
- L: Schalldruckpegel (Lautstärke) des Tons
- Lmin: niedrigster Schalldruckpegel
- Lmax: maximaler Schalldruckpegel
- nmax: Anzahl der Komponenten (Oktaven) pro Shepard-Ton
Anschließend werden die Shepard-Töne aus ihren jeweiligen Sinus-Komponenten zusammengesetzt:
\(\sum\limits_{n=1}^{n_{\mathrm{max}}}L \cdot \sin (2\pi\cdot f(m=\mathrm{const},n))\)
Die einzelnen Shepard-Töne werden nun aneinander gereiht. So entsteht eine Tonleiter oder eine einfache Melodie. Wenn Sie sich diese in einer Endlosschleife anhören, werden Sie das Gefühl bekommen, dass die Tonfolge immer höher oder tiefer wird.
Hörbeispiele zur Shepard-Skala
Der Effekt einer unendlich auf- oder absteigenden Tonleiter funktioniert mit Tonleitern, Glissandi oder einfachen Melodien. Diese Illusion wird zum Beispiel in Filmen und Computerspielen zum Spannungsaufbau genutzt. Sie könne sich die folgenden Beispiele für Shepard-Tonleitern anhören:
Unten: eine aufsteigende Melodie aus Shepard-Tönen
Quelle: Hannah Mayer
Anwendungen der Shepard-Skala
Dass ein einzelner Shepard-Ton oder eine Shepard-Skala scheinbar unendlich ansteigen oder abfallen kann, macht sie zu einzigartigen Werkzeugen in der Komposition und Sonifikation:
- In L’escalier du diable von Györgi Ligeti imitiert ein Klavier eine steigende Shepard-Skala. Eine steigende Sequenz, die einen Aufstieg repräsentiert, ist ein Beispiel für Mickey Mousing, den Sie vielleicht aus Cartoons kennen. Mehr über das künstlerisch-wissenschaftliche Wirken von Ligeti entdecken Sie im Ligeti-Zentrum in Hamburg. Die scheinbar unaufhörlich steigende Sequenz verkörpert ewiges Treppensteigen, die auch in Super Mario 64 verwendet wurde.
- In der akustischen Wasserwaage Tiltification ist die Tonhöhe konstant, wenn Sie Ihr Handy perfekt horizontal ausgelotet haben. Ist es nach rechts geneigt, fällt die Tonhöhe. Ist es nach links geneigt, steigt sie. Und zwar umso schneller, je steiler Ihr Handy geneigt ist. Liegt Ihr Handy Sekunden oder gar Minuten lang schief, muss auch der Ton minutenlang steigen oder fallen. Das kann nur der Shepard-Ton. Im CURAT Sonification Game müssen Sie den Shepard-Ton deuten, um unsichtbare Ziele zu finden.
Wenn Sie weitere spannende Informationen und Beispiele zu auditiven Illusionen finden wollen, dann lesen Sie unseren Beitrag akustische Täuschungen — Beispiele und Erklärungen.
Quellen
Shepard, R. N. (1964). Circularity in Judgments of Relative Pitch. The Journal of the Acoustical Society of America, 36(12): S. 2346–2353. https://doi.org/10.1121/1.1919362
Ziemer, T. & Schultheis, H. (2021). The CURAT Sonification Game: Gamification for Remote Sonification Evaluation. The 26th International Conference on Auditory Display (ICAD 2021): S. 233–240. https://doi.org/10.21785/icad2021.026
