In Python einen Sinus erstellen, plotten und abspielen können ist in den Musikwissenschaften und der Signalverarbeitung sehr hilfreich. Die Sinusfunktion ist eine mathematische Funktion, die sich mit einer gleichbleibenden Frequenz und Amplitude bis ins unendliche wiederholen kann. Hier erklären wir, wie Sie möglichst einfach mit Python einen Sinus plotten und abspielen können.
Python, NumPy und Matplotlib
Um in Python eine Sinus-Kurve zu definieren, zu plotten und anhören zu können brauchen Sie die folgenden Dinge:
- Die Programmiersprache Python. Sie glänzt durch ihre Vielseitigkeit und ihre große Auswahl an Bibliotheken. Die Systematische Musikwissenschaft verwendet Python zur Datenanalyse, als Basis für „Machine Learning“ oder zum Lösen von komplexen Rechenaufgaben.
- Die Python-Bibliothek NumPy dient als Grundlage für Berechnungen. Sie bietet eine Vielzahl an mathematischen Operationen, die in Python nicht enthalten sind. Ein gängiges Kürzel für numpy ist
np. - Matplotlib ist ebenfalls eine Python-Bibliothek und dient zum Darstellen von Grafiken und Diagrammen. Die Dimensionen und Seitenverhältnisse der Darstellung sind in Matplotlib sehr leicht anzupassen. Wir verwenden das Matplotlib-Modul
pyplot, im Folgenden abgekürzt alsplt. - IPython ist ein Interaktives Command-Line Interface und Teil der Entwicklungsumbgebung Jupyter. Es wird oft in der Datenanalyse verwendet und kann Audio abspielen.
Python Sinus — Funktion definieren
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Audio
samplerate = 44100
def signal(f = 440, s = 1, A = 1, phi = 1, cycles = 1):Um den Python Sinus zu definieren öffnen Sie zunächst Python in der Entwicklungsumgebung Jupyter Lab. Natürlich können Sie auch andere Umgebungen verwenden. Stellen Sie sicher, dass Numpy und Matplotlib installiert sind. IPython ist bei Jupyter Lab bereits enthalten. Importieren Sie nun Numpy, Matplotlib und IPython. Legen Sie die samplerate fest und definieren Sie dann eine Funktion mittels def signal. Die Funktion kann später mit beliebigen Werten aufgerufen werden. Hier sind die ersten Zeilen zu sehen — den gesamten Quelltext finden Sie weiter unten.
Python Sinus — Parameter
Die Funktion haben Sie nun definiert, aber wofür sind die einzelnen Variablen zuständig? Die wichtigsten Werte für den Python Sinus sind:
- Der Parameter
sampleratebeschreibt die gleichnamige Samplerate. Diese bestimmt, wie viele Punkte pro Sekunde berechnet werden. Das ist entscheidend für die Auflösung der Funktion. Standard CD-Qualität ist 44.100 Hz. Nach dem Nyquist-Theorem liegt die höchste darstellbare Frequenz bei der Hälfte dersamplerate, also in diesem Fall 22.050 Hz. Im Graphen ist diesampleraterelevant für die Auflösung der Funktion, also wie akkurat sie dargestellt wird. - Die Frequenz
fbestimmt die Tonhöhe. Meistens wird die Frequenz in Hz (also Wiederholungen pro Sekunde) angegeben. Der für Menschen hörbare Bereich befindet sich etwa zwischen 20 Hz und 20.000 Hz. - Die Zeit in Sekunden
s: Dieser Parameter beschreibt die Dauer der Funktion in Sekunden. Die Zeit bestimmt außerdem die absolute Länge der x-Achse unseres Graphen. - Die Amplitude
Abeschreibt die höchste Auslenkung des Sinus vom Nullpunkt und bestimmt die Lautstärke. Viele digitale Audio-Systeme erwarten einen Wert von null bis eins. Zum Anhören istA = 1deshalb die höchste sinnvolle Amplitude.A = 0wäre Stille. - Die Nullphase
phigibt an, in welcher Phase die Funktion anfängt. Wenn wir beispielsweisephi = 0.5angeben, verschiebt sich der Anfang der Funktion um einen halben Zyklus. - Die angezeigten Zyklen
cycles: Bei einer Frequenz von 440 Hz durchläuft der Sinus in einer Sekunde 440 Zyklen. Um den Sinus aus der Nähe betrachten zu können, ohne die Gesamtlänge des Arrays zu reduzieren, gibt es den Parametercycles. Wenncycles = 1ist, wird genau ein Zyklus des Sinus angezeigt.
Python Sinus — Rechnungen
Die wichtigsten Parameter der Funktion für den Python Sinus sind nun geklärt. Fügen Sie nun in den nächsten Zeilen die nötigen Formeln hinzu:
t = np.linspace(0, s, int(T*samplerate), endpoint=False)Benutzen Sie np.linspace, um ein Array zu erzeugen. Diese NumPy-Funktion erzeugt Punkte mit gleichem Abstand zwischen dem Startpunkt (0) und dem Endpunkt (s). Wie viele Punkte erzeugt werden, ist abhängig von der samplerate, welche Sie bereits am Anfang definiert haben. Nehmen Sie mit endpoint=False den Endpunkt heraus, damit er nicht selbst mitgezählt wird.
sine = A * np.sin(2 * np.pi * f * t - 2 * np.pi * phi)Hier kommen die Parameter von oben wieder ins Spiel. Die Amplitude A steht als Faktor vor dem Rest der Funktion. Verwenden Sie die NumPy-Funktion np.sin, um den Sinus zu erzeugen. Für π (pi) gibt es die Funktion np.pi. Die Variable f ist die Frequenz. Die Variable t repräsentiert das Array von der Zeile darüber. Alles hinter dem Minus ist für die Phasenverschiebung zuständig: Der Sinus verschiebt sich entlang der x-Achse um einen Zyklus nach rechts, wenn in der Klammer 2*np.pi abgezogen wird. Dahinter steht der Faktor zur Phasenverschiebung phi, den Sie oben in der Funktion definiert haben.
Die Variable sine repräsentiert nun ein Numpy-Array in Form einer Sinusfunktion mit allen nötigen Parametern und kann als Graph dargestellt, abgespielt oder zu einer Audio-Datei umgewandelt werden.
Den Graphen erstellen
Inzwischen haben Sie ein Array, welches alle nötigen Daten für den Python Sinus enthält. Um dieses Array in einen Graphen zu verwandeln benötigen Sie einige Funktionen von Matplotlib.
plt.figure(figsize=(10, 6))
plt.plot(t, sine)
plt.title(f'Signal:{f} Hz, Amplitude:{A}, Nullphase:{phi}')
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.grid()
plt.xlim(0, 1/(f/cycles))
plt.ylim(-A-0.5, A+0.5)
plt.axhline(0, color='black', lw=0.5, ls='--')
plt.show()
return sine
plt.figureruft den Graphen auf. Verwenden Sie im Anschlussfigsize, um die Größe des Graphen festzulegen.plt.plotlegt die Achsen fest, in diesem Fall symbolisiert die x-Achse die Zeit. Auf den durchtfestgelegten Punkten, also dersamplerate, wird dann der Sinus abgebildet.plt.titlebestimmt den Titel. Im Titel stehen alle Werte, die Sie beim Aufrufen der Funktion bestimmt haben.plt.xlabelundplt.ylabel: Legen Sie hiermit die jeweiligen Beschriftungen für die Achsen fest. Die x-Achse stellt die Zeit dar und die y-Achse die Auslenkung zum jeweiligen Zeitpunkt.plt.gridaktiviert die Hilfslinien. Damit lässt sich die Auslenkung besser ablesen.plt.xlimlegt fest, wie viel vom Graph gezeigt wird. Mit der Rechnung1/(f/cycles)können Sie einfach beim Aufrufen der Funktion entscheiden, wie viele Zyklen gezeigt werden sollen. Aus diesem Grund haben Sie vorher in der Funktioncycleseingebaut.plt.ylim(-A-0.5, A+0.5): Lassen Sie die Limitierung der y-Achse relativ zur AmplitudeAanzeigen.
Der Befehl plt.axhline vereinfacht die Visualisierung und plt.show ist nötig um den erstellten Graphen anzuzeigen. In der nächsten Zeile symbolisiert return sine das Ende der Funktion signal. Diese können Sie danach mit selbst gewählten Parametern aufrufen.
Den Python Sinus erstellen und als Audio abspielen
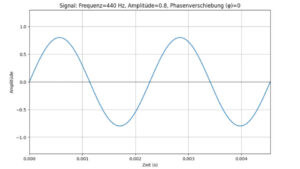
sine = signal(f = 440, s = 1, A = 0.8, phi = 0, cycles = 2)
Audio(sine, rate = samplerate)
Zuerst haben Sie die nötigen Bibliotheken importiert und den Teil der Funktion definiert, mit dem das Array bestimmt und erstellt werden kann. Danach haben Sie die Werte für den Graphen bestimmt, welcher am Ende den Sinus anzeigt. Zu guter Letzt rufen Sie in der vorletzten Zeile die erstellte Funktion mit den gewünschten Werten auf. Für diesen Schritt haben Sie am Anfang das IPython-Modul display importiert. Mit Audio rufen Sie dieses auf und geben im Anschluss die sine Variable und die samplerate an. Im Anschluss gibt Python dann einen Graphen und eine Schaltfläche zum Abspielen des Sinus aus. Das Abspielen einer Funktion als Sound nennt sich übrigens Audifikation.
Der gesamte Quelltext
Wenn Sie alle hier beschriebenen Schritte befolgt haben könnte ihr Quelltext am Ende so aussehen:
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import Audio
samplerate = 44100
def signal(f = 440, s = 1, A = 1, phi = 1, cycles = 1):
t = np.linspace(0, s, int(s*samplerate), endpoint=False)
sine = A * np.sin(2 * np.pi * f * t - 2 * np.pi * phi)
plt.figure(figsize=(10, 6))
plt.plot(t, sine)
plt.title(f'Signal: {f} Hz, Amplitude: {A}, Nullphase: {phi}')
plt.xlabel('Zeit (s)')
plt.ylabel('Amplitude')
plt.grid()
plt.xlim(0, 1/(f/cycles))
plt.ylim(-A-0.5, A+0.5)
plt.axhline(0, color = 'black', lw = 0.5, ls='--')
plt.show()
return sine
sine = signal(f = 440, s = 1, A = 0.8, phi = 0, cycles = 2)
Audio(sine, rate=samplerate)In weiteren Artikeln plotten wir einen Sinus in Matlab. Außerdem erklären Ihnen, wie Sie mittels eines Spektrogramms jede Zeitreihe in ihre Sinuskomponenten zerlegen können.
Quellen
NumPy. (n.d.). *NumPy*. [Wissenschaftliche Bibliothek für Python]. https://numpy.org/doc/stable/
Hunter, J. D. „Matplotlib: A 2D Graphics Environment“, Computing in Science; Engineering, vol. 9, no. 3, pp. 90-95, 2007. https://doi.org/10.1109/MCSE.2007.55
Fernando Pérez, Brian E. Granger, IPython: A System for Interactive Scientific Computing, Computing in Science and Engineering, vol. 9, no. 3, pp. 21-29, May/June 2007. https://ipython.org